树与二叉树
树
基本概念
树是由 N(N>=0)个有限节点组成的具有层次关系的集合,是一种简单的非栈性结构。当 N=0 时,称为空树。
数作为一种逻辑结构,同时也是一种分层结构,具有以下两个特点:
- 树的根节点没有前驱节点,除根节点以外的所有节点有且只有一个前驱结点。
- 树中可以有零个或多个后继节点
名词解释:
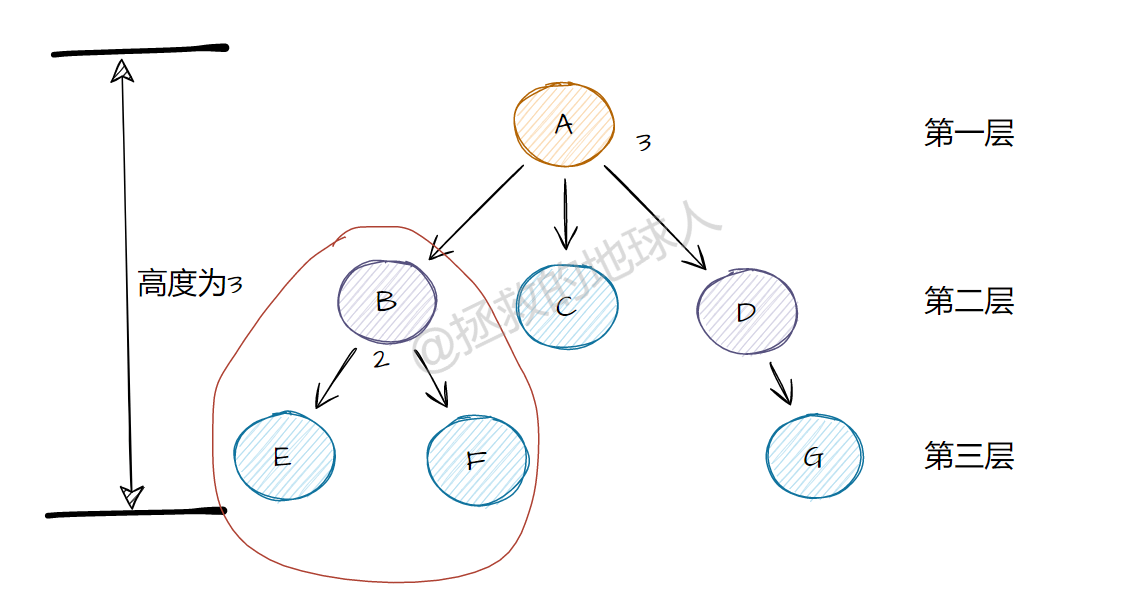
- 根节点:在树结构中,只有一个节点没有前件,称该节点为根节点(简称根)。如图 A 节点
- 父节点:在树结构中,每个节点只有一个前件,这个前进就是该节点的父节点。如图 D 节点为 G 节点的父节点
- 子节点:在树结构中,每个节点可以有多个后件,这些后件就是该节点的子节点。如图 G 节点为 D 节点的子节点
- 叶子节点:在树结构中,没有后件的节点成为叶子节点。如图 E、F、C、G 节点
- 度:树中一个节点的子节点个数成为该结点的度,树中节点的最大度数成为树的度。如图 A 节点度为 3、 B 节点为 2 则此树的度为 3
- 树的深度:在树结构中,根节点所在层次为 1,其他节点所有的层次为其父节点所在的层次加 1,最大的层次成为树的深度。如图深度为 3
- 子树:在树结构中,以某一个节点的一个子节点为根节点构成的树,成为该节点的子树。如图红色圆圈区域为一个字数
性质
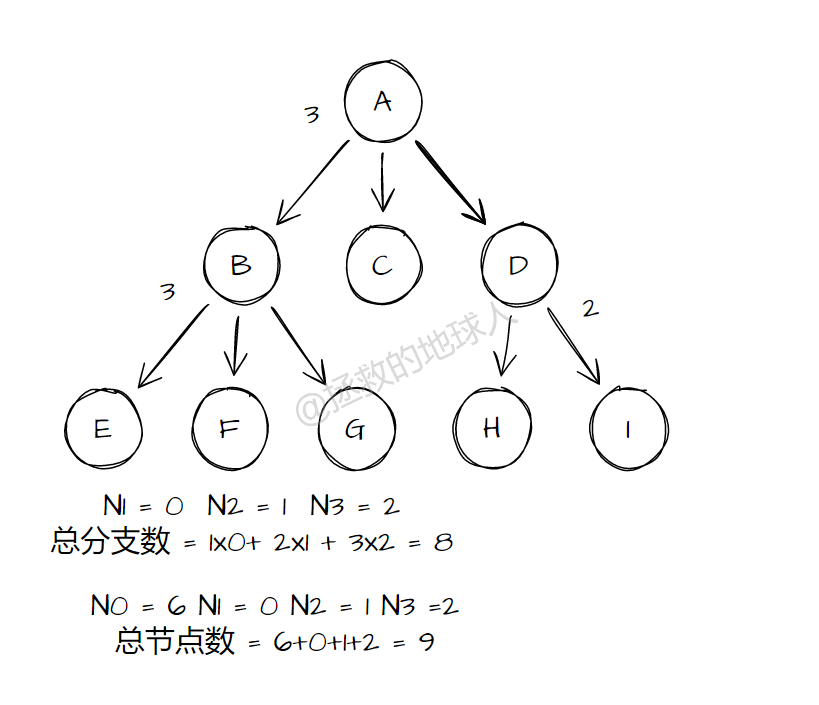
- 总分支树:
1*N^1 + 2*N^2 + 3*N^3 + ... + m*N^m(度为 m 的节点引出的 m 条分支) - 总节点数:
N0+N1+N2+N3+N4 + ... + Nm - 树中的节点数等于所有节点度加 1
- 度为 m 的树中第 i 层至少有 mi - 1 节点(i>=1)
二叉树
基本概念
二叉树是另一种树形结构,其特点是每个节点至多只有两颗子树(即二叉树中不存在度大于 2 的节点)。并且,二叉树的子树有左右之分,其次序不能颠倒。
二叉树是 n(n>0)个节点有限集合:
- n = 0 为空二叉树
- n > 1 二叉树由一个根节点和两个互不相交的被称为左子树和右子树组成,左子树和右子树分别是一颗二叉树
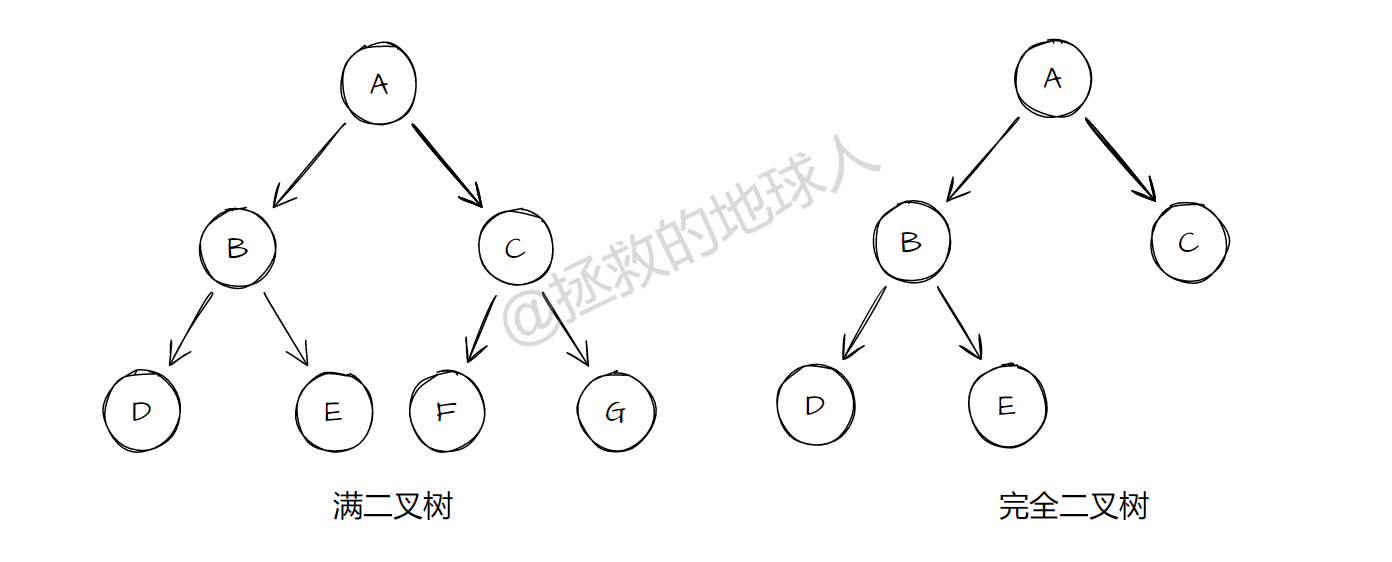
满二叉树
满二叉树的叶子节点都集中在二叉树的最下一层,除叶子节点以外每个节点的度数都是 2。总节点数 2^h - 1
完全二叉树
深度为 K,有 n 个节点的二叉树当且仅当其每一个结点都与深度为 K 的满二叉树一一对应,称为完全二叉树
- 叶子节点从右开始缺
- 完全二叉树可以是满二叉树
性质
- 非空二叉树上的叶子节点数等于度为 2 的节点数加 1,即 N0 = N2 + 1
- 非空二叉树上第 K 层至多有 2^(K-1)个节点(K > 1)
- 高度为 H 的二叉树至多有 2(H-1)个节点(H > 1)
- 具有 N(N > 0)个节点的完全二叉树的高度为 log2(N+1) 向上取整 或 log2N + 1 向下取整
存储结构
二叉树的存储结构分为顺序存储和链式存储:
顺序存储:二叉树的顺序存储是用一组连续的存储单元存放二叉树中节点元素,一般按照二叉树节点自上而下、自左向右的顺序存储。(为空元素留出空间)
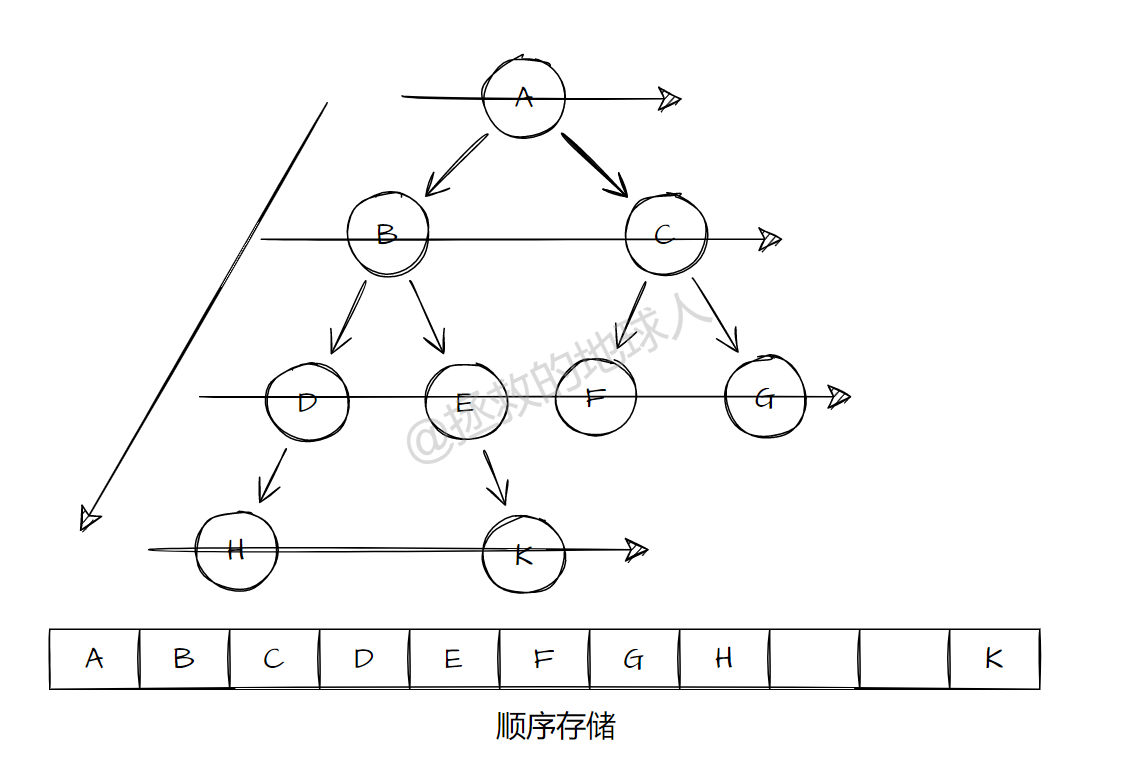
链式存储:二叉树的链式存储结构是用一个链表来存储一颗二叉树,二叉树中每一个节点用链表的一个链节点来存储。
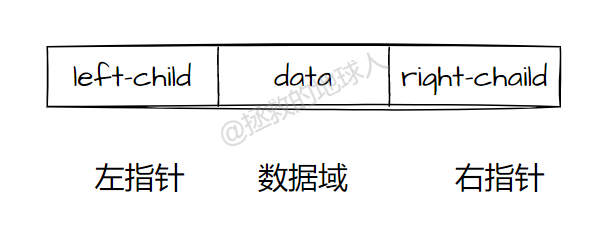
*遍历方法
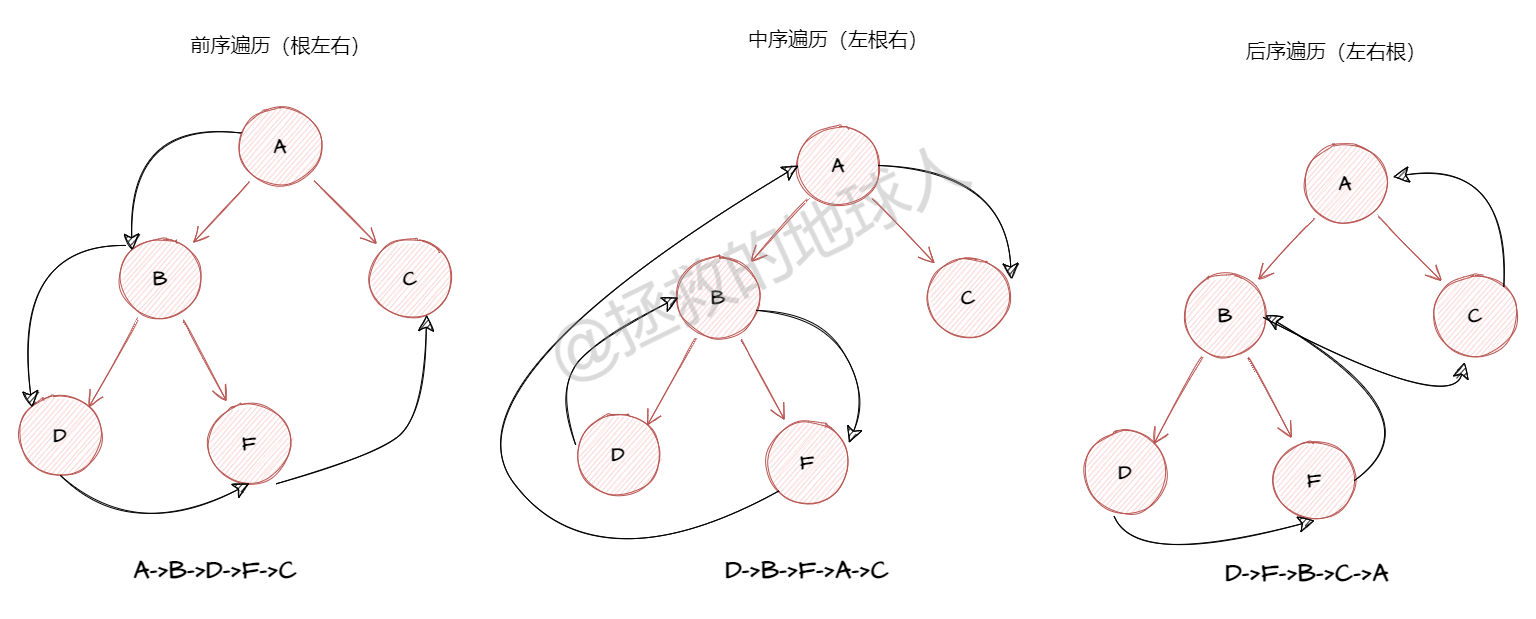
所谓二叉树的遍历,是指按某条搜索路径访问树中的每个节点,是的每个节点均被访问一次,并且仅被访问一次。常见的三种遍历算法分别是前序遍历、中序遍历、后序遍历
- 前序遍历(DLR)(根 左 右):首先访问根节点,其次左子树,最后右子树
- 中序遍历(LDR)(左 根 右):首先访问左子树,其次访问跟节点,最后右子树
- 后序遍历(LRD)(左 右 根):首先访问左子树,其次右子树,最后根节点
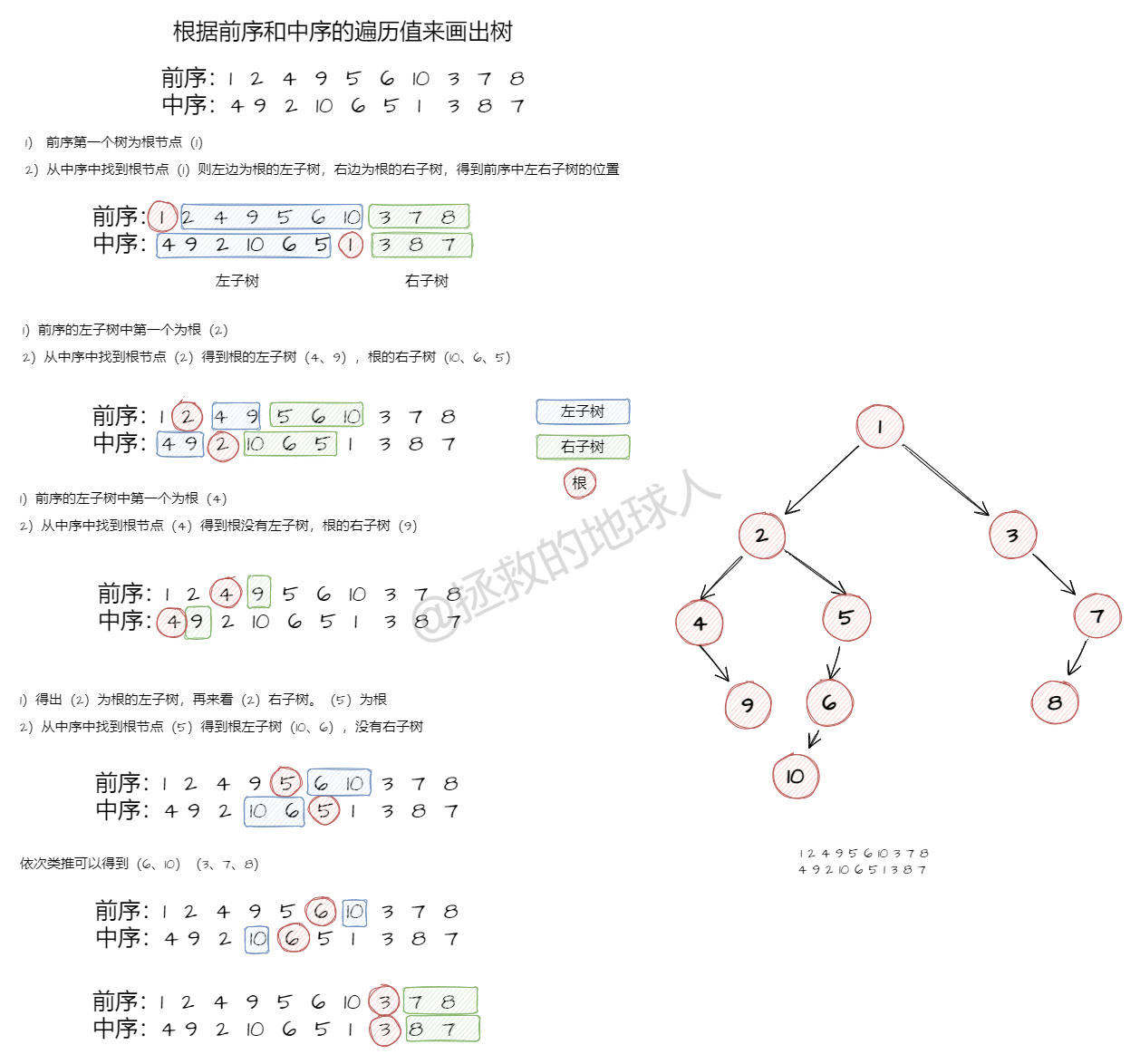
算法题
根据前序和中序的遍历值来画出树,前序:1/2/4/9/5/6/10/3/7/8 中序:4/9/2/10/6/5/1/3/8/7。
解析过程
144 二叉树的前序遍历
解析过程
思路:前序遍历,根左右深度优先遍历,root
递归
var preorderTraversal = function (root) {
if (!root) return [];
let res = [];
function dps(r) {
if (!r) return null;
res.push(r.val);
dps(r.left);
dps(r.right);
}
dps(root);
return res;
};
迭代
var preorderTraversal = function (root) {
if (!root) return [];
let stack = [root];
let res = [];
while (stack.length) {
let r = stack.pop();
if (r) {
res.push(r.val);
stack.push(r.right);
stack.push(r.left);
}
}
return res;
};
94 二叉树的中序遍历
解析过程
递归
var inorderTraversal = function (root) {
if (!root) return [];
let res = [];
function dps(r) {
if (!r) return;
dps(r.left);
res.push(r.val);
dps(r.right);
}
dps(root);
return res;
};
迭代
var inorderTraversal = function (root) {
if (!root) return [];
let stack = [];
let res = [];
while (root || stack.length) {
while (root) {
stack.push(root);
root = root.left;
}
let cur = stack.pop();
res.push(cur.val);
root = cur.right;
}
return res;
};
145 二叉树的后序遍历
解析过程
递归
var postorderTraversal = function (root) {
if (!root) return [];
let res = [];
function dps(r) {
if (!r) return null;
dps(r.left);
dps(r.right);
res.push(r.val);
}
dps(root);
return res;
};
迭代
var postorderTraversal = function (root) {
if (!root) return [];
let res = [];
let stack = [];
let pre = null;
//主要思想:
//由于在某颗子树访问完成以后,接着就要回溯到其父节点去
//因此可以用prev来记录访问历史,在回溯到父节点时,可以由此来判断,上一个访问的节点是否为右子树
while (root || stack.length) {
while (root) {
stack.push(root);
root = root.left;
}
//从栈中弹出的元素,左子树一定是访问完了的
let node = stack.pop();
//现在需要确定的是是否有右子树,或者右子树是否访问过
//如果没有右子树,或者右子树访问完了,也就是上一个访问的节点是右子节点时
//说明可以访问当前节点
if (node.right == null || pre == node.right) {
res.push(node.val);
pre = node;
node = null;
} else {
//如果右子树没有被访问,那么将当前节点压栈,访问右子树
stack.push(node);
root = node.right;
}
}
return res;
};
589 N 叉树的前序遍历
104 二叉树的最大深度
617 合并二叉树
543 二叉树的直径
105 从前序与中序遍历序列构造⼆叉树
226 翻转二叉树
103 二叉树的锯齿形层序遍历
331 验证二叉树的前序序列化
解题思路
连续两个# 代表前一个是叶子节点。
如果遇到两个 #则说明前一个节点为叶子节点
删除两个 #, 并将叶子节点替换为 #
110 平衡二叉树
107 二叉树的层序遍历 II
236 二叉树的最近公共祖先
102 二叉树的层序遍历
114 二叉树展开为链表
96 不同的二叉搜索树
98 验证二叉搜索树
解题思路
- 二叉搜素树对应中序遍历(左跟右) 左边最小、其次根、右边最大。
- 对 root 进行中序遍历,取值跟上一个值进行比较,如果小就返回 false。
662 二叉树最大宽度
解题思路
- 根节点编号 n 左子节点 2n 右子节点 2n+1
- 深度优先遍历 每层的最左边是最先遍历到。利用 map 记录其编号(当前层最小编号)
- 后续遍历过程取值进行比对
var widthOfBinaryTree = function (root) {
let map = new Map();
let ans = 0;
function dfs(r, u, depth) {
if (!r) return;
if (!map.has(depth)) map.set(depth, u);
ans = Math.max(ans, u - map.get(depth) + 1);
u = u - map.get(depth) + 1;
dfs(r.left, u << 1, depth + 1);
dfs(r.right, (u << 1) | 1, depth + 1);
}
dfs(root, 1, 0);
return ans;
};